Introduction to Randomization and Layout

Randomization and Layout

Randomization, or random distribution of treatments into experimental units, helps ensure that measurements of experimental variation are unbiased by destroying correlations among errors. When an entire treatment is grouped together; for example, on the sunny side of greenhouse, lighting becomes a confounding factor to actual treatment. Even if statically significant differences are detected between treatments, it is impossible to differentiate treatment effects from lighting effects. Random allocation of treatments to different physical locations helps to spread error equally and disrupt any possible spurious correlations among errors due to environmental variation. The layout of an experiment refers to the physical arrangement of experimental units in space. Experimental layouts can be either completely randomized or blocked arrangements.

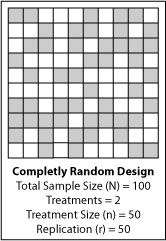
Completely Randomized Design

The simplest experimental layout is a completely randomized design. This layout works best in tightly controlled situations with small experimental error; where the experimental units are fairly homogeneous, and the environmental conditions within the physical space of the experiment are uniform. The statistical analysis of completely randomized designs is simple and will tolerate some missing data. The disadvantage of a completely randomized design is that anticipated variation cannot be excluded from experimental error.

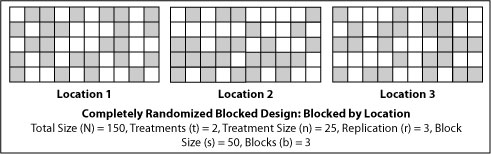
Blocked Designs

Often investigators anticipate highly recognizable covariates (sources of variation not due to treatment response). For example, plots nearest each other in field experiments and greenhouse benches can be expected to respond similarly due to common environmental conditions. In animal studies, factors like weight, age, and sex can often be expected to increase experimental variation. When an investigator expects a source a variation that is not a treatment response, the layout of the experiment can be grouped, or blocked, to minimize within block variations and increase between block variations. Blocking allows for statistical control of experimental error by adjusting treatment means proportionally to between block error. Experiments can be blocked for any factor, including technicians. When multiple people are involved in an experiment, assigning a block to every technician can minimize differences in personal technique.

A completely randomized block design will fully replicate all treatments in grouped homogeneous blocks. In field research, location is often a blocking factor (See more on Randomized Complete Block Design and Augmented Block Design).

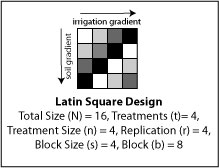
Latin square design is a form of complete block design that can be used when there are two blocking criteria. This is layout is used in field experiments when environmental gradients, such as irrigation and soil type, are expected to differ by rows and by columns. Every treatment is randomly assigned once in every row and every column. Each row and each column are complete blocks. The major disadvantage to this layout is that the number of rows and columns must be equal.

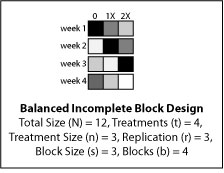
Incomplete block designs are useful when time and/or space is not adequate to monitor all treatments at one time. Incomplete block designs allow for experiments to be conducted in stages. Additionally incomplete block designs can reduce experimental error for more precise treatment comparison; even more so than a complete block design.

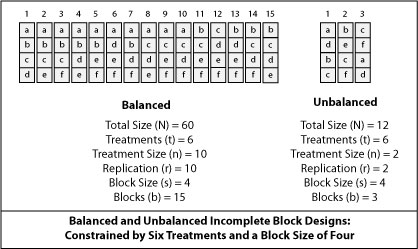
A balanced incomplete block design will compare all treatments with equal precision, because every treatment pair occurs together equal amounts of time. Consider that an investigator wants to compare three fertilizer treatments (0, 1X, 2X) on four cultivars, replicating the experiment three times. Space is limited to only three treatment by cultivar combinations at a time. A balanced incomplete block design, as illustrated below, accommodates the need to preform this experiment in stages.

An unbalanced incomplete block design can also be used when an experiment is preformed in stages. An unbalanced design allows for a smaller experiment at the expense of precision, because not every treatment pair occurs together equal amounts of time. Increasing the repetitions of an unbalanced incomplete block design will improve precision. Replicating an unbalanced experiment may still result in a smaller experiment than a balanced design. The unbalanced incomplete block design illustrated below is small enough to repeat up to four times and still remain smaller than the balanced design. 

Funding Statement

Development of this page was supported in part by the National Institute of Food and Agriculture (NIFA) Solanaceae Coordinated Agricultural Project, agreement 2009-85606-05673, administered by Michigan State University. Any opinions, findings, conclusions, or recommendations expressed in this publication are those of the author(s) and do not necessarily reflect the view of the United States Department of Agriculture.